
易経「繋辞上伝」を読み解く22
子曰く、易を作る者は、其(そ)れ盗(とう)を知るか。易に曰く、負(お)うて且つ乘(の)る。寇(あだ)の至るを致すと。負ふとは、小人の事也。乘るとは君子の器也。小人にして君子の器に乘れば、盗、之を奪はんことを思ふ。上(かみ)には慢にして下(しも)には暴なれば、盗、之を伐たんとことを思ふ。藏(ぞう)を慢にするは盗を誨(おし)へ、容を冶(かざ)るは淫(いん)を誨(おし)ふ。易に曰く、負(お)うて且つ乘(の)る。寇(あだ)の至るを致すと。盗を之招く也。(繋辞上伝第8章第11節)
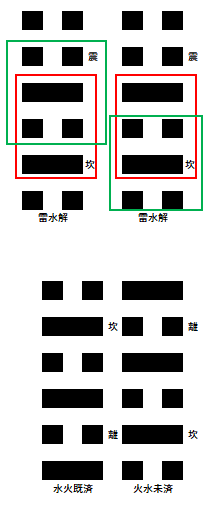
孔子が最後に引用する「雷水解」は実に味わい深い卦です。
互體には二爻から四爻を「離」三爻から五爻までを「坎」と取ればこれは「水火既済」であり、一方で初爻から三爻までの「坎」と、二爻から四爻までの「離」を併せれば「火水未済」となります。
完成であり、そこが到達点。
しかし終着点ではない。
君子の道に終わりはなく、易経も「火水未済」から再び「乾為天」に戻り、生成化育の次の循環が始まるように、さらに次の高みを目指すのだと孔子は諭す。
雷水解の三爻の爻辞「 負(お)うて且つ乘(の)る。寇(あだ)の至るを致す 」とは、分不相応なふるまいを戒める爻辞です。
悟りを得た、君子の道に至ったとそこで成長を辞めてしまえば、後からその道を歩んでくる、かつその歩みを止めない者にたちまちその地位を追われてしまうことを、財を見せびらかして盗みに遭う愚か者、あるいは淫らな容姿を振りまいて姦淫に遭う婦人に例えこれを戒めます。
「 易を作る者は、其(そ)れ盗(とう)を知るか。 易に曰く、負(お)うて且つ乘(の)る。寇(あだ)の至るを致すと。 小人にして君子の器に乘れば、盗、之を奪はんことを思ふ。上(かみ)には慢にして下(しも)には暴なれば、盗、之を伐たんとことを思ふ。 藏(ぞう)を慢にするは盗を誨(おし)へ、容を冶(かざ)るは淫(いん)を誨(おし)ふ。易に曰く、負(お)うて且つ乘(の)る。寇(あだ)の至るを致すと。盗を之招く也。 」

「易経を作った伏羲は、世の中で“盗み”という所業が絶えない仕組みを良く理解していたのだ。“雷水解”の三爻に“身分の卑しい者が、貴人の乗る車に乗っている。分不相応な行いは盗みに遭うような災いを招き寄せる”とある。
そもそも移動は徒歩である庶民と異なり、車に乗ることを許されるような身分の高い者は、周囲からの尊敬を一身に集めるような徳を身に着けているし、その徳には盗みに遭うような災いを退けるような高い“威徳”を併せ持っている。
しかし、その威徳を自分より立場が上の者に対して傲岸不遜、自分より立場の弱い者に対しては増長傲慢にふるまう事だと勘違いするような小人であれば、たちまち他者の恨みを買って、その地位や財を奪って懲らしめてやろうと思う者が現れるはずだ。
財あることをこれ見よがしに他者に見せびらかせば、これを盗んでくれと言わんばかりに見えるし、婦人が艶めかしく容姿を彩れば、図らずもそれを見る者には男を誘っている淫らな女性と見えてしまう。だから“雷水解”三爻に“ 負(お)うて且つ乘(の)る。寇(あだ)の至るを致す ”とこれを戒める。分不相応なふるまいは、災いを招くと」

雷水解の卦は上卦と下卦を入れ替えると「水雷屯」となります。
この卦は64卦の乾為天と坤為地の次に来る3番目の卦であり、植物の種子が水を得て固い殻を破って芽を出すが、まず先に土中の根を伸ばし、表土の上の枝葉は根が伸びるまではその成長をとどめる様に、「初心忘るべからず」と戒める卦であり、全陽、全陰の乾坤を除いた陰陽交わる始まりの卦でもあります。
雷水解の卦辞に「西南に利し。往く所旡ければ、其れ来たり帰りて吉」とあり様々な苦難を乗り越え至った君子の道に、一息を付くことは許されても、「往く攸(ところ)有れば、夙(はや)くして吉なり」と一時的な休息は許されても、その歩みを止めてはならないと次の出立を促します。
雷水解に込められた「水火既済」と「火水未済」には、悟りの境地に至った君子にその感慨にふける時は許されても、そこが終着点ではなく植物が種子を遺しその種子が来春芽を結ぶように、次の道に向けその一歩を踏み出すことを促している、その意を込めて孔子はこの卦を引用した7卦最後に引用したのでしょう。


↓繋辞上伝を読み解く23↓














コメント